

 Cao Jingzhong (1937- ) is a native of Xuzhou, Jiangsu province. He is research fellow of Marine Geology and Earth Physics Department, Tongji University. He graduated from Mathematics Department, Jiangsu Normal College (currently known as Suzhou University) in 1963. In the 1970s, he took up research on geophysics prospecting. In the 1980s, he engaged in study on methods of handling the data of seismic prospecting and led state key projects in "Sixth 5-Year Plan" and "Seventh 5-Year Plan". In 1991, he was awarded Tan Kah Kee Award in Geosciences for "Development of Seismic Migration Theory and Practice" as a second completer. He was also awarded State Science and Technology Progress Award, Second Class for "Seismic Migration Imaging Theory and 3-D P-R Migration Technology and its Application in Oil and Gas Prospecting and Developing". He was awarded Science and Technology Achievement, Third Class by China Ministry of Geology and Mineral Resources for "Tau-p field Parameter Extraction Method".
Cao Jingzhong (1937- ) is a native of Xuzhou, Jiangsu province. He is research fellow of Marine Geology and Earth Physics Department, Tongji University. He graduated from Mathematics Department, Jiangsu Normal College (currently known as Suzhou University) in 1963. In the 1970s, he took up research on geophysics prospecting. In the 1980s, he engaged in study on methods of handling the data of seismic prospecting and led state key projects in "Sixth 5-Year Plan" and "Seventh 5-Year Plan". In 1991, he was awarded Tan Kah Kee Award in Geosciences for "Development of Seismic Migration Theory and Practice" as a second completer. He was also awarded State Science and Technology Progress Award, Second Class for "Seismic Migration Imaging Theory and 3-D P-R Migration Technology and its Application in Oil and Gas Prospecting and Developing". He was awarded Science and Technology Achievement, Third Class by China Ministry of Geology and Mineral Resources for "Tau-p field Parameter Extraction Method".
DEVELOPMENT OF SEISMIC MIGRATION THEORY AND PRACTICE
Ma Zaitian
(Tongji University, Shanghai)
Abstract
None of the large and middle oii fields in the world has been discovered without using the technique of seismic prospecting after the World War II The main work of studying the subsurface structures is the seismic migration processing with large computer. The modern seismic migration technique was pioneered by J.F. Claerbout at the Stanford University in the 1970s.His equation adapts to only single geological structure with dip angles 0o -- 15o.
To break out the dip limitation of Claerbout's equation we put forward a new theory, method and technique, which are playing an important role in the completion of modern seismic imaging technique. The idea and method described here have been popularized in China and abroad.
For the best imaging seismic observation data we worked out a new higher-order partial differential equation and its solution. The solution was obtained by using our 'order-splitting' method. The higher-order partial differential equation used in seismic migration was derived as follows:
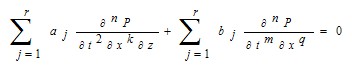 (1)
(1)
where n is the order number of the equation; i=1, 2, 3???, r[r=(n+1)/2),if n is odd; r=n/2, if n is even]; =n-1, n-2, n-3, ??? , r; k=0,2,4, ??? , r; j=1, 2, 3, ??? , s (s=n-r); m =1, 3, 5, ??? , if n is odd; m=0, 2, 4, ??? , if n is even ; q=2,4,6, ???.
The equation (1) is a new type of partial differential equation; it cannot be solved by conventional method. We proposed a new scheme called order-splitting method to solve it. In numerical mathematics, the dimension-splitting method has been used, but the order-splitting method is not existed before. By the order-splitting method the high-order equation (1) can be transformed into a system of second-order partial differential equations:
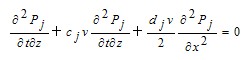 (2)
(2)
j=1,2,3, ??? , n-1.
Each equation in (2) is a parabolic-type equation. We have proved that it is well- posed and stable in computation. The system of equations (2) is equivalent to the original equation (1).
The method was tested by theoretical and practical seismic data, and the results show that the order-splitting method is excellent in seismic migration. The research has scientific and practical useful value. It has been playing an important role in the study of complex geological subsurface structures for exploration and production of oil and gas in every region where they exist.